Our introductory post on literacy’s connection to different academic subjects included the role of reading in mathematics. Every subject brings specialized vocabulary that students must master on their way to proficiency. Math is no exception. Success in specific domains, such as geometry and algebra, is strongly linked to the early acquisition of vocabulary knowledge (Peng & Lin, 2019). The relationship between reading and math goes far beyond vocabulary, however. Students in Grades K–12 are increasingly asked to describe and justify their mathematical thinking, which places a premium on language and literacy skills outside of reading instruction (Rittle-Johnson et al., 2017).
One of the clearest examples of math’s literacy demands—and one of the biggest stumbling blocks for students—is the word problem. Solving word problems involves reading comprehension, the ability to filter out irrelevant information, and the ability to plan and execute a solution strategy. This post explains why word problems are difficult for many students and why common strategies fail.
The Problem With Word Problems
A word problem is a question in which relevant operations (e.g., addition, division) and numbers must be obtained from written text (Verschaffel et al., 2020). Word problems differ from computational problems, in which students’ solutions are based on mathematical notation (e.g., “+,” “-;” Powell et al., 2022). In contrast, solving word problems involves comprehending text, interpreting visuals (e.g., figures, tables), organizing ideas, and relating this information to math. The ability to solve word problems represents one of the key indicators of mathematical competence for elementary school students (Powell et al., 2021). Word problems are especially challenging for students with math-related learning disabilities, who may struggle with reading comprehension, math vocabulary, and interpreting visual supports (Arsenault & Powell, 2022).
Unfortunately, word problems are made more daunting by the continued dissemination of ineffective strategies (Hegarty et al., 1995). A particularly prominent example is the keyword strategy, which involves (a) identifying specific words in the problem text and (b) selecting an operation based on their presence. For example, when using the keyword strategy, students may learn that words like “total” and “more” signal addition or that words like “difference” and “left” signal subtraction. The following problem features a keyword commonly associated with addition (i.e., “in total”). A student might be capable of finding the correct solution using only the numbers and keywords:
Lena has 8 pencils. She buys 5 more at the store. How many pencils does she have in total?
In total = +
8 + 5 = 13
As is clear from our example, the keyword strategy can be effective for basic problems with a single operation; however, it quickly becomes counterproductive as problems become more challenging (Powell et al., 2022). The table below illustrates how commonly taught keyword-operation associations can lead to errors in problem solving:
| Keyword | Assumed Operation | Why It’s Misleading | Example |
| Total | Addition | Not exclusive to addition | A farmer has 4 baskets with 6 apples each. How many apples are there in total? = 4 × 6, not 4 + 6 |
| More | Addition | Not exclusive to addition | Tom has 12 marbles. He has 4 more than Jake. How many marbles does Jake have? = 12 – 4, not 12 + 4 |
| Difference | Subtraction | Not exclusive to subtraction; appears in multistep problems | A store sold 120 tickets on Saturday and twice as many on Sunday. What is the difference in tickets sold? Student may incorrectly subtract 120 − 2 = 118, instead of computing 2 × 120 = 240, then 240 − 120 = 120. |
| Left | Subtraction | Could mean a result after multiple steps | Anna baked 12 cookies and then baked 8 more. She gave 10 away. How many does she have left? Student may incorrectly solve for 12 − 10 = 2, instead of (12 + 8 ) – 10 = 10 |
| Each | Multiplication | Not exclusive to multiplication | Each student gets 3 pencils. If there are 24 pencils, how many students can get pencils? = 24 ÷ 3, not 24 × 3 |
| Per | Division | Used in rates or ratios, which may involve multiple operations | Gas costs $3 per gallon. How much do 5 gallons cost? = 3 × 5, not 3 ÷ 5 |
Additional limitations with the keyword strategy include:
1. Finding Words Isn’t Reading.
Unlike conventional elementary-level reading passages, which may contain familiar content or predictable structures, word problems often feature unfamiliar language and sentence structures the reader must comprehend before obtaining the solution (Karp et al., 2019). In this sense, word problems are more difficult than typical reading tasks, as extracting information requires close attention to each sentence. The keyword strategy, however, effectively encourages students to avoid reading entirely, suggesting that—much like a computational problem—the presence of a symbol or word (e.g., “total,” “difference,” “+,” “-“) is sufficient.
A student applying the keyword strategy to the following simple problem, in which “in total” signals the use of addition:
Lena has 8 pencils. She buys 5 more at the store. How many pencils does she have in total (+)?
is effectively being encouraged to interpret the problem like this:
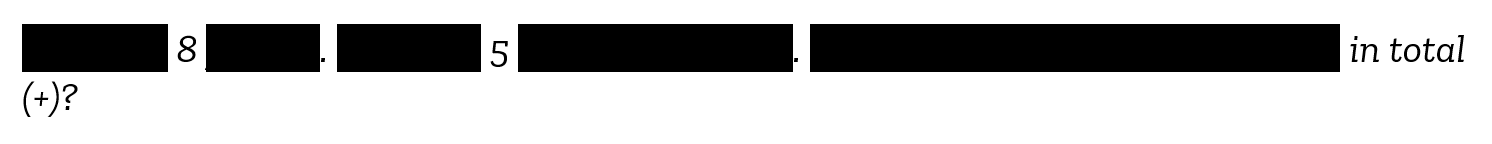
The keyword strategy bypasses comprehension by prompting students to search for words rather than to read for understanding. This may have dubious appeal for students who struggle with reading, have limited working memory, or who are only solving simple problems. However, the strategy is ineffective when applied to more advanced problems (Powell et al., 2022).
2. Supposed Keywords Can Misdirect Students or Leave Them Stranded.
Many simple problems, even those with keywords, require the full context of the passage to arrive at the correct answer (Karp et al., 2019):
A gardener plants 6 rows of flowers, with 14 flowers per row. How many flowers are there in total?
The above problem might be quickly solved using multiplication. Students who employ the keyword strategy and isolate the phrase “in total” in these instances may incorrectly apply addition:

In other cases, problems may lack keywords entirely:
There are 30 apples in the basket. If 12 are green, how many are red?
This can paralyze the learner or lead to guessing:
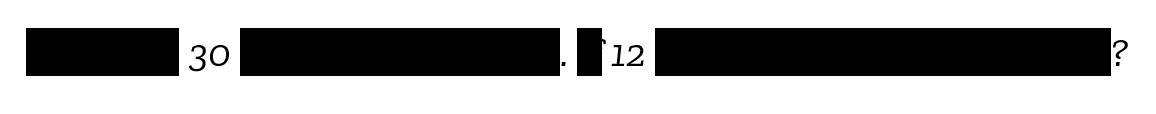
3. Keywords Cannot Be Used for Complex, Multistep Problems.
The simple problems shown earlier are largely absent from the curriculum by the middle-elementary grades (Karp et al., 2019). Problems with multiple steps quickly become the norm:
Maya picked 15 apples in the morning and 8 more in the afternoon. She gave 10 apples to her friend. How many apples does she have in all?
Attempting to solve the previous problem using apparent keywords (e.g., more = +; gave = -; in all = +):
Maya picked 15 apples in the morning and 8 more (+) in the afternoon. She gave (-) 10 apples to her friend. How many apples does she have in all (+)?
may prompt the student to apply operations in the wrong order, or to use irrelevant operations:
15 + 8 + 10 = 33
15 - 10 = 5
In the long term, solving word problems correctly requires the integration of literacy skills with mathematical content and processes. Students must receive effective strategies as early as possible, before the difficulty of problems becomes overwhelming. In our next post on literacy and mathematics, we’ll cover two evidence-based approaches to word problems: attack strategies and schema instruction.
Acknowledgement
We thank Sarah Powell, Professor of Special Education at the University of Texas at Austin, whose presentation at the UI Baker and Teacher Leader Center in February 2025 greatly informed this post.
References
Arsenault, T. L., & Powell, S. R. (2022). Word-problem performance differences by schema: A comparison of students with and without mathematics difficulty. Learning Disabilities Research & Practice, 37(1), 37–50. https://doi.org/10.1111/ldrp.12273
Hegarty, M., Mayer, R. E., & Monk, C. A. (1995). Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. Journal of Educational Psychology, 87(1), 18–32. https://doi.org/10.1037/0022-0663.87.1.18
Karp, K. S., Bush, S. B., & Dougherty, B. J. (2019). Avoiding the ineffective keyword strategy. Teaching Children Mathematics, 25(7), 428–435.
Peng, P., & Lin, X. (2019). The relation between mathematics vocabulary and mathematics performance among fourth graders. Learning and Individual Differences, 69, 11–21. https://doi.org/10.1016/j.lindif.2018.11.006
Powell, S. R., Berry, K. A., Fall, A. M., Roberts, G., Fuchs, L. S., & Barnes, M. A. (2021). Alternative paths to improved word-problem performance: An advantage for embedding prealgebraic reasoning instruction within word-problem intervention. Journal of Educational Psychology, 113(5), 898–910. https://doi.org/10.1037/edu0000513
Powell, S. R., Namkung, J. M., & Lin, X. (2022). An investigation of using keywords to solve word problems. The Elementary School Journal, 122(3), 452–473. https://doi.org/10.1086/717888
Rittle-Johnson, B., Loehr, A. M., & Durkin, K. (2017). Promoting self-explanation to improve mathematics learning: A meta-analysis and instructional design principles. ZDM, 49, 599–611. https://doi.org/10.1007/s11858-017-0834-z
Verschaffel, L., Schukajlow, S., Star, J., & Van Dooren, W. (2020). Word problems in mathematics education: A survey. ZDM, 52, 1–16. https://doi.org/10.1007/s11858-020-01130-4
